2485 - 最长不下降子序列
描述
小杨有个包含 n 个节点 m 条边的有向无环图,其中节点的编号为 1 到 n。
对于编号为 i 的节点,其权值为 w_i。对于图中的一条路径,根据路径上的经过节点的先后顺序可以得到一个节点权值的序列,小杨想知道图中所有可能序列中最长不下降子序列的最大长度。
注:给定一个序列 S,其最长不下降子序列 S' 是原序列中的如下子序列:整个子序列 S' 单调不降,并且是序列中最长的单调不降子序列。例如,给定序列 S = [11,12,13,9,8,17,19],其最长不下降子序列为 S'=[11,12,13,17,19],长度为 5。
输入
第一行包含两个正整数 n,m,表示节点数和边数。
第二行包含 n个正整数 A_1, A_2, \dots A_n,表示节点 1 到 n 的点权。
之后 m 行每行包含两个正整数 u_i, v_i,表示第 i 条边连接节点 u_i 和 v_i,方向为从 u_i 到 v_i。
输出
输出一行一个整数表示答案。
样例
输入
5 4 2 10 6 3 1 5 2 2 3 3 1 1 4
输出
3
输入
6 11 1 1 2 1 1 2 3 2 3 1 5 3 4 2 2 6 3 6 1 6 4 6 1 2 5 1 5 4
输出
4
输入
6 11 5 9 10 5 1 6 5 4 5 2 4 2 3 1 5 3 6 1 4 1 4 3 5 1 2 3 2 1
输出
4
提示
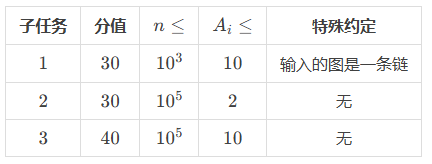
对全部的测试数据,保证 1 \leq n \leq 10^5,1 \leq m \leq 10^5,1 \leq A_i \leq 10。