1941 - 植树
Description
Ysuperman 有一棵 n 个节点的无根树 T。如果你不知道树是什么,TA 很乐意告诉你,树是一个没有环的无向联通图。
既然树是无根的,那就没有办法种植。Ysuperman 研究了很久的园艺,发现一个节点如果可以成为根,它必须十分平衡,这意味着以它为根时,与它**直接相连的节点,他们的子树大小都相同**。
你作为幼儿园信息组一把手,Ysuperman 给你一棵树,你能在 1s 内找到所有可能成为根的节点吗?
Input
第一行一个正整数 n,表示树的节点个数。
此后 n-1 行,每行两个正整数 u_i,v_i,表示树上有一条直接连接 u_i,v_i 的边。保证每条边只会给出一次。
Output
不超过 n 个从小到大的整数,用空格隔开,表示每一个可能成为根的节点。
Examples
Input
2 1 2
Output
1 2
Input
4 1 2 2 3 3 4
Output
1 4
Input
9 1 2 1 3 4 1 5 1 1 6 1 9 8 1 1 7
Output
1 2 3 4 5 6 7 8 9
Hint
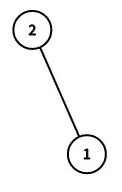
样例1说明:
以 1 为根时,与 1 直接相连的点有 \{2\},因为只有一个所以大小全部相同。
以 2 为根时,与 2 直接相连的点有 \{1\},因为只有一个所以大小全部相同。
所以答案为 1,2。
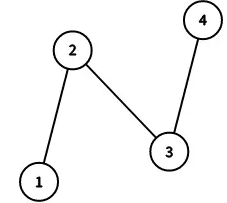
样例2说明:
以 1 为根时,与 1 直接相连的点有 \{2\},因为只有一个所以大小全部相同。
以 2 为根时,与 2 直接相连的点有 \{1,3\},子树大小分别为 \{1,2\},不相同。
以 3 为根时,与 3 直接相连的点有 \{2,4\},子树大小分别为 \{2,1\},不相同。
以 4 为根时,与 4 直接相连的点有 \{3\},因为只有一个所以大小全部相同。
所以答案为 1,4。
数据范围:
对于 50\% 的数据,满足 1 \le n\le 10^4。
对于 100\% 的数据,满足 1 \le n\le 10^6。