1899 - E满二叉树的距离
Description
我们有一棵顶点为 2^N-1 的树。
顶点编号为 1 到 2^N-1。每个 1\leq i < 2^{N-1} 都有以下边:
- 连接顶点 i 和顶点 2i 的无向边、
- 连接顶点 i 和顶点 2i+1 的无向边。
没有其他边。
假设两个顶点之间的距离是连接这两个顶点的简单路径中的边的数量。
求模为 998244353 的顶点 (i, j) 中,两顶点间的距离为 D 的顶点对的数目。
Input
输入两个数字N,D
Output
输出一个值
Examples
Input
3 2
Output
14
Input
14142 17320
Output
11284501
Hint
样例解释:
下图描述了给定的树。
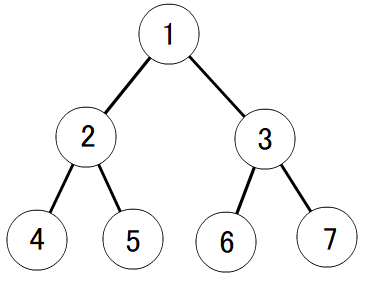
有 14 对顶点,它们之间的距离是 2:(1,4),(1,5),(1,6),(1,7),(2,3),(3,2),(4,1),(4,5),(5,1),(5,4),(6,1),(6,7),(7,1),(7,6).
数据范围:
- 2 \leq N \leq 10^6
- 1 \leq D \leq 2\times 10^6
- 所有数据都是整数范围。