给定一个长度为 n 的序列 A_i。定义 W_{l,r} 为 A_l , A_{l+1}, · · · , A_{r−1}, A_r 内出现奇数次的元素的异或和。

例如序列 A = {3, 5, 3, 6, 7}，W_{1,4} = 5 ⊕ 6 = 3。

现在给定 q 次询问，每次 询问给出两个参数 l, r，求出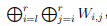，每个区间的 W_{l,r} 的异或和。

第一行两个整数 n, q。 

第二行 n 个整数，第 i 个整数代表 A_i。 

接下来 q 行，每行两个整数，表示此次询问的 l, r。

共 q 行，每行一个整数，第 i 行表示第 i 次询问的答案。

测试点1-3:  1 \leq n,q \leq 10

测试点4-5:  1 \leq n,q \leq 1000

测试点6-10:  1 \leq n,q \leq 2 \times 10^5,0 \leq A_i \leq 10^9

样例1解释：

i=1，j=1，2

i=2，j=2

1^1^2^2=0

其实就是双重循环，应该能够理解了吧！