1408 - 最大割
Description
给定一张有 n 个点、m 条边的无向图,如果有一种划分,能将图上的所有点不重复不遗漏地分割成两个部分(记为 S 与 \bar{S} ),且这两部分都不是空集,则称 (S,\bar{S})) 是图的一个割(Cut)。
对于一个割来说 (S,\bar{S})),图上有多少边跨越这个割,这个割的大小就是多少。所谓跨越,就是指某条边的一端在 S,另一端在 \bar{S}。
对于给定的图,请找到一个最大的割,并输出这个割的大小。
Input
第一行:两个整数表示 n 与 m;
第二行到第 m+1 行:每行两个整数 u 与 v 表示一条边的两个端点,保证 u\neqv,注意同一对点之间可能有多条边,这些边应被看做是不同的边。
Output
单个整数:表示最大割的大小
Examples
Input
3 5 1 2 2 3 3 1 1 3 2 3
Output
4
Input
4 2 1 2 3 4
Output
2
Hint
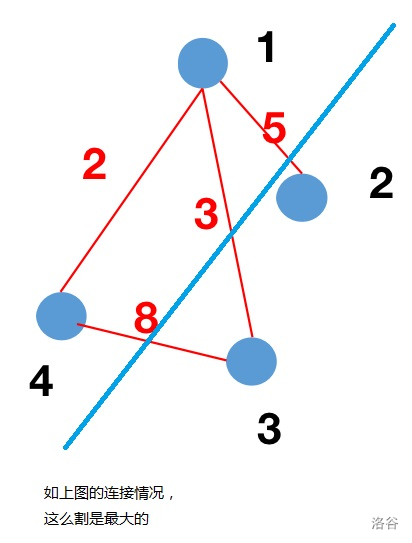
### 样例1中
将图割成{1,2}与{3},1与3之间有两条边,2与3之间也有两条边。
### 样例2中
将图割成{1,3}与{2,4}时割最大。注意与最小割的区别,这个例子中的最小割为0(因为{1,2}与{3,4}不连通)
```
50%数据 2=<n<=16
100%数据 2=<n<=24
100%数据 1=<m<=1000