拼接单词

题目大意：求 A 的前缀和 B 的后缀拼接起来能组成多少个字符串。

首先，绝大部分的答案字符串都是不重复的，我们只需要求出来有多少重复的就可以了。

只有 A 和 B 中出现相同的字符，才会出现相同的答案字符串。

样例：

A : tree

B : heap

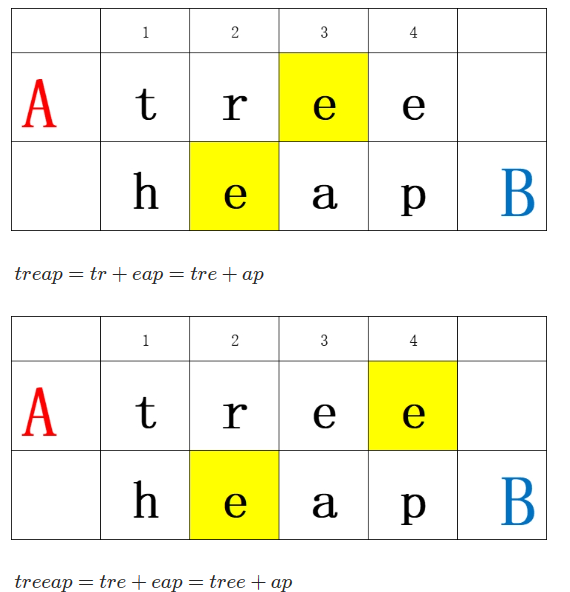
有两种重复的字符串，而一共有 4*4=16个字符串，于是答案是 16-2=14。

若有一对相同的字符， 就会有一对相同的字符串。而字符只有 26 个，可以参考桶的思想，线性扫一遍两个数组中每个字符的数量，对于每个字符计算会有多少的重复字符串，时间复杂度为 O(N+M)

特殊地，题目要求答案字符串中须同时包含 A 的前缀和 B 的后缀，不能仅包含一个，所以 A 的第一个字符和 B 的最后一个字符是都在每个答案字符串中的，所以无需查询这两个元素。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
string a,b;
ll n,m,cnta[27],cntb[27],cnt;
int main(){
	cin>>a>>b;
	n=a.size(); m=b.size();
	a=" "+a; b=" "+b;
	for(int i=2;i<=n;i++) cnta[a[i]-'a'+1]++;
	for(int i=1;i<=m-1;i++) cntb[b[i]-'a'+1]++;
	for(int i=1;i<=26;i++) cnt+=cnta[i]*cntb[i];
	cout<<n*m-cnt<<endl;
	return 0;
}

八进制小数

#include <cstring>
#include <iostream>
using namespace std;
char s[510];
int a[1105], b[1105], ans[3005];
int main () {
	a[1100] = 1;
	scanf ("%s", s + 1);
	int len = strlen (s + 1);
	for (int i = 1; i <= len; i ++) {
		for (int j = 1100; j >= 1; j --) a[j] *= 125;
		for (int j = 1100; j >= 1; j --) {
			a[j - 1] += a[j] / 10;
			a[j] %= 10;
		}
		if (s[i] != '0') {
			int t = s[i] - 48, fir;
			for (int j = 1100; j >= 1; j --) b[j] = a[j] * t;
			for (int j = 1100; j >= 1; j --) {
				b[j - 1] += b[j] / 10;
				b[j] %= 10;
				if (b[j] != 0) fir = j;
			}
			int size = 1101 - fir;
			int na = 3 * i + 1 - size, nb = fir;
			while (nb != 1101) {
				ans[na] += b[nb];
				na ++;
				nb ++;
			}
			for (int i = 3000; i >= 1; i --) {
				ans[i - 1] += ans[i] / 10;
				ans[i] %= 10;
			}
		}
	}
	int tmp = 0;
	for (int i = 3000; i >= 1; i --)
		if (ans[i] != 0 && !tmp) tmp = i;
	for (int i = 1; i <= tmp; i ++) cout << ans[i];
	return 0;
}

树的最长路

#include <bits/stdc++.h>

using namespace std;

const int N = 200010;

struct node {
    int to, nxt, wt;
} eg[N * 2];

int n;
int far, mx;
int dp[N];
int ans[N];
int hd[N], tot;

void add(int u, int v, int w) {
    eg[tot].to = v;
    eg[tot].wt = w;
    eg[tot].nxt = hd[u];
    hd[u] = tot++;
}

void dfs(int u, int pre) {
    for (int i = hd[u]; i != -1; i = eg[i].nxt) {
        int v = eg[i].to, w = eg[i].wt;
        if (v != pre) {
            dp[v] = dp[u] + w;
            ans[v] = max(ans[v], dp[v]);
            if (dp[v] > mx)
                mx = dp[v], far = v;
            dfs(v, u);
        }
    }
}

int main() {
    cin >> n;
    tot = 0, mx = -1;
    for (int i = 0; i <= n; ++i)
        hd[i] = -1, ans[i] = 0;
    for (int i = 2, v; i <= n; ++i) {
        scanf("%d", &v);
        add(i, v, 1), add(v, i, 1);
    }
    dp[1] = 0;
    dfs(1, 0);
    dp[far] = 0;
    dfs(far, 0);
    dp[far] = 0;
    dfs(far, 0);
    for (int i = 1; i <= n; ++i) {
        if (i == far) printf("%d", mx);
        else printf("%d", ans[i]);
        putchar(' ');
    }
    return 0;
}

最大频率

这个题目其实就是区间最值问题，你可以用线段树，分块，st等等来做！

这里面有一个关键词，就是数据是不降的，所以，我们会发现相同的数字肯定会在一起，所以可以考虑进行数字记录！

#include<cmath>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int M=1e5+10,len=512;

int n,q,a[M],lsh[M];
int L[len],R[len],bel[M];
int pre[len][M];//前 i 块中数字 j 共出现 pre[i][j] 次
int ans[len][len];//第 i~j 块中的众数共出现 ans[i][j] 次

void build(){
    int size=sqrt(n);
    for(int i=1;i<=n;i++) bel[i]=(i-1)/size+1;
    for(int i=1;i<=bel[n];i++) L[i]=(i-1)*size+1,R[i]=i*size;
    R[bel[n]]=n;

    for(int i=1;i<=bel[n];i++){
        for(int j=1;j<=lsh[0];j++) pre[i][j]=pre[i-1][j];
        for(int j=L[i];j<=R[i];j++) pre[i][a[j]]++;
    }
    for(int i=1;i<=bel[n];i++)
        for(int j=i;j<=bel[n];j++){
            ans[i][j]=ans[i][j-1];
            for(int k=L[j];k<=R[j];k++)
                ans[i][j]=max(ans[i][j],pre[j][a[k]]-pre[i-1][a[k]]);
        }
}

int buc[M];
int query(int l,int r){
    int p=bel[l],q=bel[r],ret=0;
    if(q-p<=1){
        for(int i=l;i<=r;i++) buc[a[i]]++;
        for(int i=l;i<=r;i++) ret=max(ret,buc[a[i]]);
        for(int i=l;i<=r;i++) buc[a[i]]=0;
    }else{
        ret=ans[p+1][q-1];
        for(int i=l;i<=R[p];i++) buc[a[i]]++;
        for(int i=L[q];i<=r;i++) buc[a[i]]++;
        for(int i=l;i<=R[p];i++) ret=max(ret,pre[q-1][a[i]]-pre[p][a[i]]+buc[a[i]]);
        for(int i=L[q];i<=r;i++) ret=max(ret,pre[q-1][a[i]]-pre[p][a[i]]+buc[a[i]]);
        for(int i=l;i<=R[p];i++) buc[a[i]]=0;
        for(int i=L[q];i<=r;i++) buc[a[i]]=0;
    }
    return ret;
}

int main(){
    scanf("%d%d",&n,&q);
    for(int i=1;i<=n;i++) scanf("%d",&a[i]);

    for(int i=1;i<=n;i++) lsh[++lsh[0]]=a[i];
    sort(lsh+1,lsh+1+lsh[0]);
    lsh[0]=unique(lsh+1,lsh+1+lsh[0])-lsh-1;
    for(int i=1;i<=n;i++) a[i]=lower_bound(lsh+1,lsh+1+lsh[0],a[i])-lsh;

    build();
    for(int i=1,l,r;i<=q;i++){
        scanf("%d%d",&l,&r);
        printf("%d\n",query(l,r));
    }
    return 0;
}