祖孙询问

30分做法：裸奔LCA或者各种暴力

100分做法：

DFS序以及各种求LCA算法均可秒杀此题。

DFS遍历树，记录每个点X的第一次访问时间st[x]和最后一次访问时间ed[x],若y在以X为根的子树中，则一定有st[x]<st[y]<ed[y]<ed[x]。

比赛

根据期望的和=和的期望，只需把A队每个人的期望得分减去B队每个人的期望得分即为答案。

A队某人X的期望得分为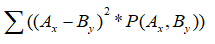（其中y为B队中实力低于X的人，P代表X和Y相遇的概率）。

显然任意两个人相遇的概率是相等的，=两人第一场相遇的概率+两人第一场不相遇的概率*两人第二场相遇的概率+……。

30分做法：任意枚举两个人算期望。

100分做法：排序后只需枚举一个人i，用一个指针指着另一 队中实力比i弱的里面最强的人，维护实力值的前缀和，实力值平方的前缀和即可算出期望。

显然指针只可能向右移动，所以这一步是线性的。

数字

ANS=前n位之和与后n位之和相等的方案数+奇数位之和与偶数位之和相等的方案数-前n位之和与后n位之和相等且奇数位之和与偶数位之和相等的方案数

前2个需要+的方案数都很好求，直接递推，重点是最后一个要满足2个条件的方案数怎么求，其实也很简单：

因为前n位之和=后n位之和，奇数位之和=偶数位之和

所以前n位中奇数位之和=后n位中偶数位之和 且

 前n位中偶数位之和=后n位中奇数位之和

现在只要求上面这个问题的方案数，由于两个等式中的元素无交集，也是十分好算的。