1216 - 卡车加油

普通的队列是一种先进先出的数据结构，元素在队列尾追加，而从队列头删除。优先队列是一种按照优先级决定出队顺序的数据结构，优先队列中的每个元素被赋予级别，队首元素的优先级最高。

例如： 4 入队， 1 入队，入队，此时队首元素不是而是，这是因为默认最小的元素优先级最高。此时如果选择出队，那么是出队。

优先队列的实现方法有很多，最简单常见的是利用“堆”这个数据结构来实现。所以我们先从堆排序开始讲起。

堆排序

堆排序（英语： Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。
使用堆排序对一组数进行排序，主要分为2步：

建堆，复杂度 O(n)，建堆的过程类似体育比赛中的淘汰赛，两个一组进行淘汰，选出优胜者。然后再对优胜者分组，两个一组进行淘汰...直到只剩下唯一的优胜者。整个过程需要比较 n/2+n/4+n/8+... 次，所以复杂度为 O(n)。
从堆顶逐个取出元素，并对堆进行维护，每次取值并维护的复杂度为 O(log(n))，因此堆排序的总复杂度为 O(nlog(n))。

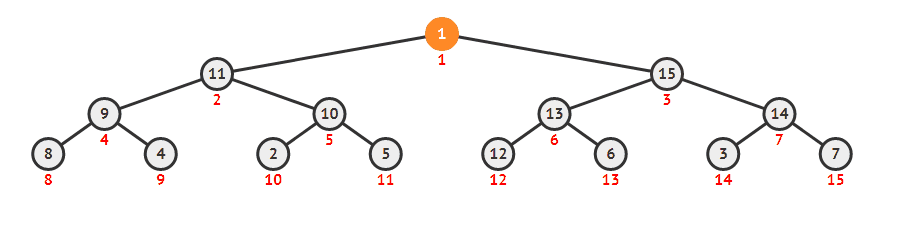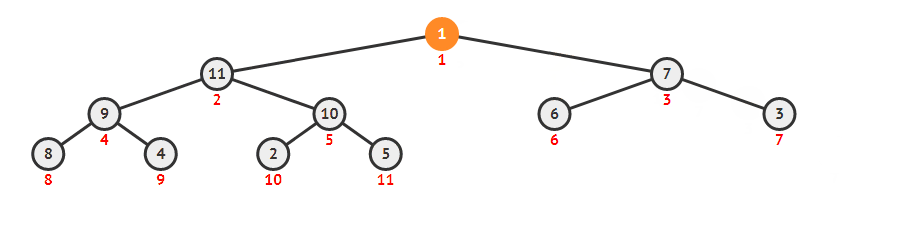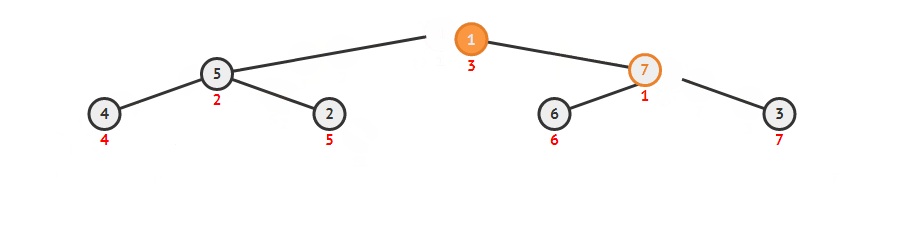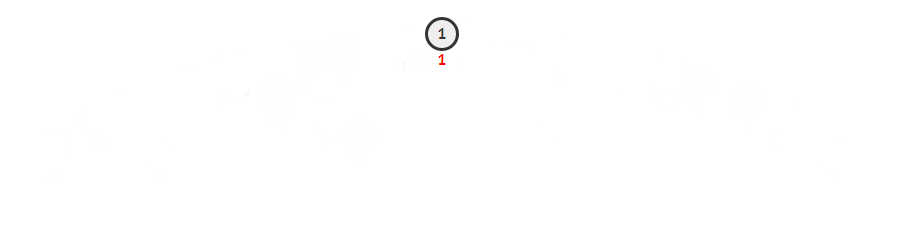
大根堆

能够用来做优先队列的数据结构有很多，平衡树，二项堆，左偏树，斐波那契堆......我们只介绍最简单的大根堆。
大根堆利用了与堆排序类似的方法。建堆后每次可以用 O(log(n))的时间取出最大数。

堆的存储及建堆

直接使用数组来存储堆，我们始终将和 an/2中较大的数，放在 an/2的位置上。

添加堆元素

直接将新的元素放在最后一个位置上 an ，同时按照建堆时的方法，比较 an 和 an/2 ， an/ 和 an/4，... 这样可以在 O(log(n)) 的复杂度维护好堆。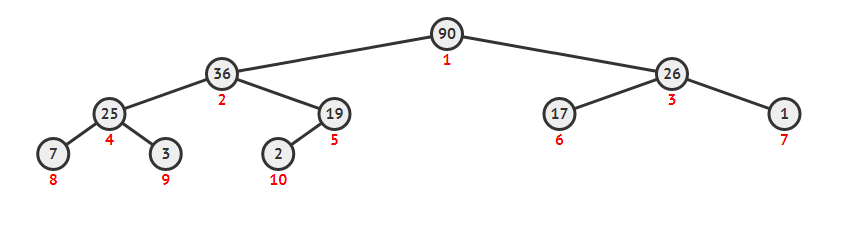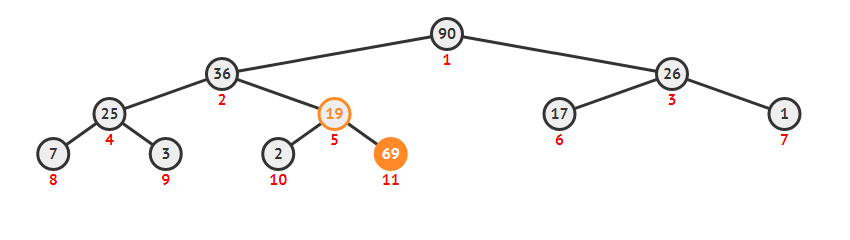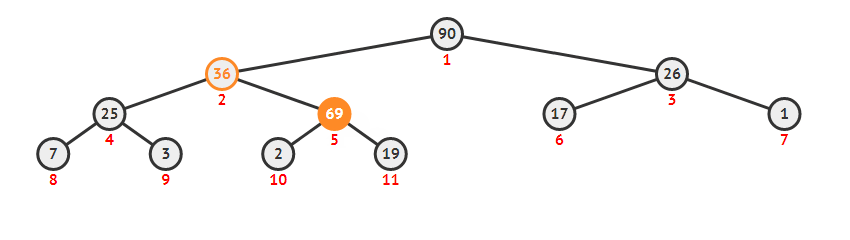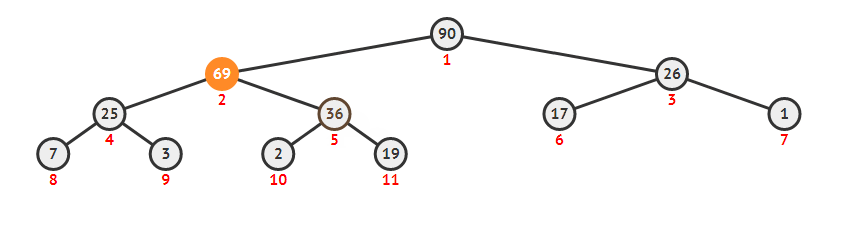

堆取最大

直接读取 a0 ，复杂度 O(1)。

堆删除最大

删除最大值需要维护堆，这个复杂度是 O(log(n))的。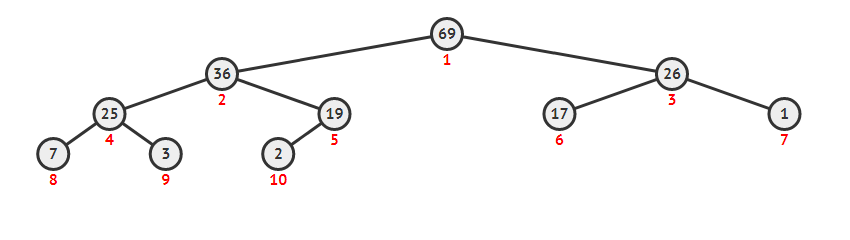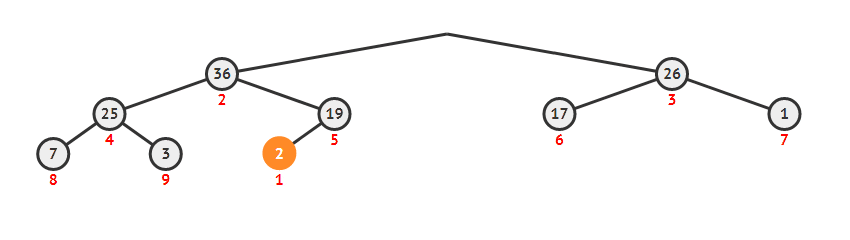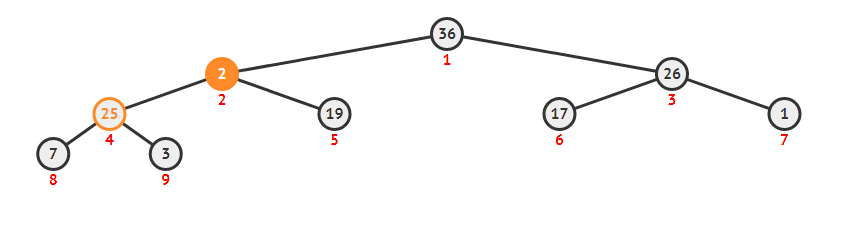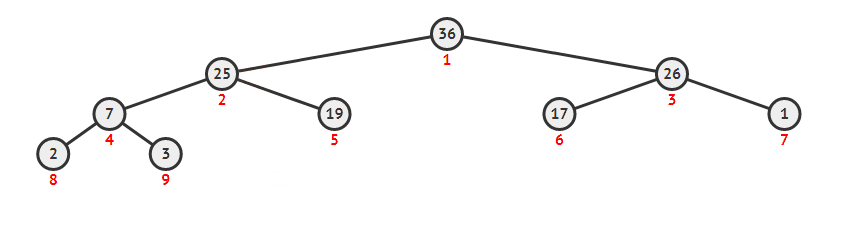

	取最大	添加	删除最大
数组	O(n)	O(1)	O(n)
链表	O(n)	O(1)	O(n)
排序好的数组	O(1)	O(n)	O(1)
大根堆	O(1)	O(log(n))	O(log(n))

stl的优先队列

虽然我们讲了很多大根堆的知识，但实际并不需要我们手写一个大根堆， C++ 的 Stl中直接提供了可以调用的优先队列， Stl中的优先队列就是采用大根堆来实现的。
//优先队列需要头文件
#include<queue>
// 定义优先队列
priority_queue<结构类型> 队列名;
priority_queue <int> q;
priority_queue <double> d;
//优先队列的操作
q.size();//返回q里元素个数
q.empty();//返回q是否为空，空则返回1，否则返回0
q.push(k);//在q的末尾插入k
q.pop();//删掉q的第一个元素
q.top();//返回q的第一个元素

使用优先队列

以上如何使用 stl 中的优先队列。以下为具体示例。

 #include<cstdio>  
#include<queue>  
using namespace std;
priority_queue <int> q;
int main() 
{
q.push(10), q.push(8), q.push(12), q.push(14), q.push(6);
 while (!q.empty()) {
 cout << q.top() << " ";
q.pop();
}
}

程序大意就是在这个优先队列里依次插入 10、8、12、14、6 ，再输出。
输出的结果就是：
14 12 10 8 6
也就是说，它是按从大到小排序的！

less和greater优先队列

还是以 int 为例，先来声明：

 priority_queue <int,vector<int>,less<int> > p;
priority_queue <int,vector<int>,greater<int> > q;

less 是从大到小， greater是从小到大。

在卡车开往终点的过程中，只有在加油站才可以加油。但如果转换成：在到达加油站 i时，就获得了一次在之后任何时候都可以加 B[i]单位汽油的权利。在解决问题上是一样的。

想要加油的次数尽可能少，当燃料用完时，假如我们此时有多个可以选择的 B[i]，根据贪心的思想，应该选油量 B[i] 最大的加油站。

因此需要一直动态的维护一个可供选择的 B[i]列表，这就应用到了优先队列的性质。

那么算法的设计如下：

当经过加油站时，将 B[i]加入优先队列中。
如果燃料为 0 。
如果优先队列为空，则表示无油可加，无法到达终点。
否则取出优先队列中最大的元素，用来给卡车做次加油。