1181 - 区间中的最大值
RMQ( Range Maximum Query )问题是指:对于长度为 n 的数列 A ,回答若干询问 Q(A,i,j)(i,j<=n),返回数列 A 中下标在 (i−>j)里的最大值。 RMQ问题是指求区间最值的问题。
RMQ问题有多种解决方式,不同方法的复杂度不尽相同。这里只讲解最简单的 ST 表的方法。
假如用暴力方式求解的话,共 T 次查询,每次查询区间 (i,j),暴力是 O(n) 的,因此总的复杂度为 O(T×n)。是无法通过评测的。
区间最大不能像前缀和一样,用前缀最大来处理。那么如何来做预处理呢?
一个表不够的话,我们就用多个表来做。假如数组长度为 n ,我们用 log(n)个表来做预处理。
St[i][k]用来记录以第 i个数为开始,长度为 2k的区间内的最大值。
所以有:
St[i][k]=Max(St[i][k−1],St[i+2k−1][k−1])
这样我们可以通过一个 O(nlog(n))的预处理,得到这 log(n)个表的所有值。
例如: {9,13,3,5,21,17,1,11}
| St[i] | |
|---|---|
| St[0] | {9,13,3,5,21,17,1,11} |
| St[1] | {13,13,5,21,21,17,11} |
| St[2] | {13,21,21,21,21} |
| St[3] | {21} |
有了这个表后,任意一段区间 (i,j)的最值,可以拆分为 2 个值 St[i][k],St[j−2k−1][k]中取较大的。
前一段区间 (i,i+2k−1) 中的最大值为: St[i][k](以 i 开头)
后一段区间 (j−2k+1,j)中的最大值为: St[j−2k−1][k] (以 j结尾)
且 2 段区间的并集,刚好覆盖 (i,j)。
这样,区间最大的查询,可以 O(1) 完成。
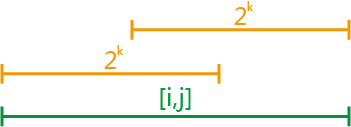
例如:查询区间为 (4,17),区间总长度为 14 ,相当于询问 (4,11) 和 (10,17) 这两个区间(长度均为 8 )最大值的最大值。而这 2 段区间的最大值都已经通过预处理提前求出来了,我们从 St 中找到对应的长度 8 ,再分别找到 4,10两个位置具体的值,就可以 O(1)求出区间 (4,17) 的最大值了。
以上就是 RMQ问题的 St 表解法。