2237 - 传送阵portal
描述
现在有一个 n \times m 的方格图。每个方格上铭刻了一个有编号的传送阵。
Alice 初始位于方格图的一个位置,她想要移动到另一个位置。
Alice 每次可以选择:
- 花费一个金币,移动到上下左右相邻的方格中;
- 不花费金币,使用传送阵,传送到具有\textbf{相同编号传送阵}的方格中。
Alice 只能\textbf{至多}传送 k 次。
现在Alice想知道她最少要花费多少金币。
输入
第一行三个正整数 n, m, k,表示方格图的大小为 n 行 m 列,Alice 最多可以传送 k 次。
第二行四个正整数,前两个正整数 x_1, y_1 表示Alice的初始位置(x_1 行 y_1 列),后两个正整数 x_2, y_2 表示Alice想要到达的位置(x_2 行 y_2 列)。
接下来 n 行,每行 m 个数字,表示方格图上每个位置所铭刻的传送阵的编号。
输出
一行一个正整数,表示Alice最少需要花费多少金币
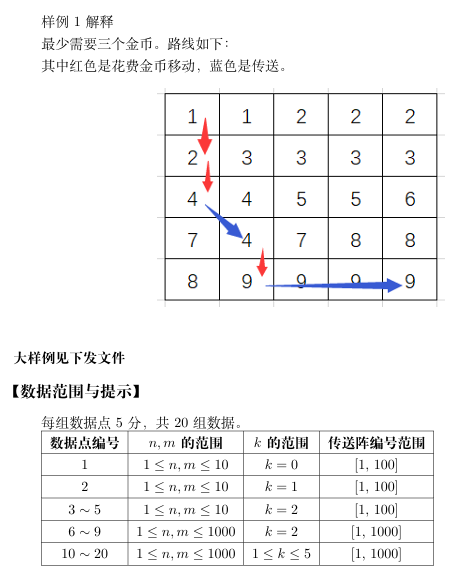
样例
输入
5 5 2 1 1 5 5 1 1 2 2 2 2 3 3 3 3 4 4 5 5 6 7 4 7 8 8 8 9 9 9 9
输出
3