2084 - 树的联通节点
描述
给你一棵树,树上有 N 个顶点,编号为 1 到 N 。 i -th 边连接顶点 A_i 和 B_i 。
考虑从这个图中删除一些边和顶点(可能为零)后可以得到一棵树。求这样一棵树中包含所有 K 指定顶点 V_1,\ldots,V_K 的顶点的最小数目。
输入
一个数字N和K;
接下来N行,每行两个数字u和v,表示u和v的连边
最后一行k个数字,表示指定的k个点
输出
最少需要几个点,才能保证链接
样例
输入
7 3 1 2 1 3 2 4 2 5 3 6 3 7 1 3 5
输出
4
输入
4 4 3 1 1 4 2 1 1 2 3 4
输出
4
输入
5 1 1 4 2 3 5 2 1 2 1
输出
1
提示
- 1 \leq K \leq N \leq 2\times 10^5
- 1 \leq A_i,B_i \leq N
- 1 \leq V_1 < V_2 < \ldots < V_K \leq N
- 给定图形是一棵树。
- 所有输入值均为整数。
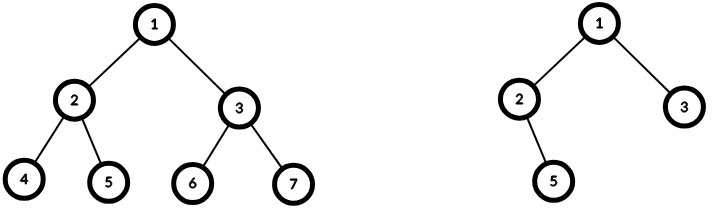
样例1说明:
下图左边显示的是给定的树。右图是包含所有顶点
1,3,5 的顶点数最少的树。