早晨, 小 \mathrm{Guan} 舒适地坐在湖边的岸上, 致力于他最喜欢的爱好一一钓鱼。他注意到平静的湖面上有许多萤火虫在飞行。小 \mathrm{Guan} 非常喜欢这样的风景, 因此决定将其作为照片拍下来。
小 \mathrm{Guan} 的相机拍摄的照片都是正方形的。拍照之前, 小 \mathrm{Guan} 可以将相机水平放置在任意高度, 并将其左右或上下移动。但是, 小 \mathrm{Guan} 不想旋转它, 以免照片歪斜。相机还配备了用于放大或缩小的变焦功能。
小 \mathrm{Guan} 希望湖面上所有的的萤火虫都能在照片中 (边界上也算)。他想使用缩放功能来设置照片的参数, 以使萤火虫尽可能大。小 \mathrm{Guan} 愿意稍等片刻, 直到最佳的拍摄时机, 但等待时间必须是非负整数秒。
为了稍微简化问题, 我们可以假设所有萤火虫始终处于同一平面内, 并且平行于相机的平面, 而且每一个萤火虫都在做匀速直线运动。
第一行包含一个正整数 n , 表示萤火虫的数量。
接下来 n 行, 每行四个整数 x_{i}, y_{i}, a_{i}, b_{i}, 表示一只萤火虫, 初始位置为 \left(x_{i}, y_{i}\right), 在 t 秒后将会位于 \left(x_{i}+t a_{i}, y_{i}+t b_{i}\right) 。
输出一行一个非负整数, 即照片边长的最小值。
输入
4 4 0 -1 1 1 6 -1 -2 -1 -5 0 2 -1 -1 1 1
输出
3
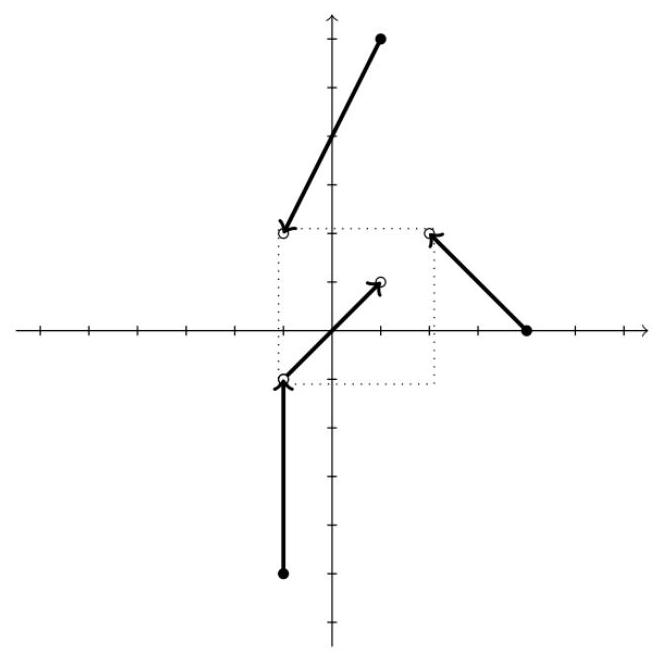
该图显示了萤火虫的初始位置及其在两秒内的飞行路线。其中边长为 3 的边平行坐标轴的正方形包含了所有萤火虫。
对于 100 \% 的数据, \left|x_{i}\right|,\left|y_{i}\right|,\left|a_{i}\right|,\left|b_{i}\right| \leq 100000 。
| 测试点编号 | n | 约定 |
| :--- | :--- | :--- |
| 1,2 | =2 | 无 |
| 3,4,5 | \leq 100000 | a_{i}=b_{i}=0 |
| 6,7,8,9,10 | \leq 100000 | 无 |