1191 - N皇后V2
描述
在 n*n 格(n<=15)的国际象棋棋盘上摆放 n 个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法。
在原来的程序中,我们用二维数组记录每个棋子的位置。逐行放置棋子,每次需要循环 1−n,来判断某列是否已经被占用。再 2次循环 1−n,判断两个斜线上是否已经放置了棋子。
如何用位运算加速这个判断呢?我们用 3个整数来分别记录列、左斜线、右斜线棋子被占用的情况,我们以 6 皇后为例
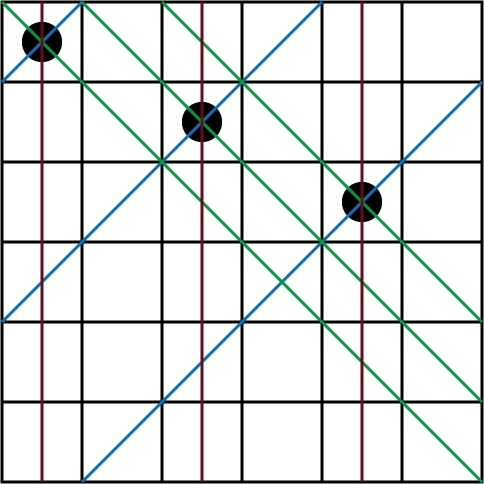
和普通算法一样,程序一列一列地寻找可以放皇后的地方。函数带三个参数 row,lvis,rvis ,分别表示在纵列和两个对角线方向的限制条件下这一行的哪些地方不能放。位于该行上的冲突位置就用 row,lvis 和 rvis 中的 1 来表示。把它们三个或起来,得到该行所有的禁位,取反后就得到所有可以放的位置(用 pos 来表示)。
| 二进制表示 | 棋子位置 | |
|---|---|---|
| 列 | 101010 | 1,3,5 |
| 右上到左下( lvis ) | 100100 | 1,4 |
| 左上到右下( rvis ) | 000111 | 4,5,6 |
| 所有禁放位置( pos) | 100111 | 1,4,5,6 |
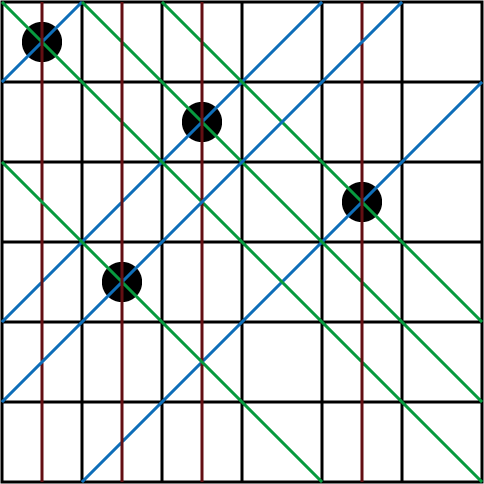
| 列( row) | 111010 | 1,2,3,5 |
| 右上到左下( lvis) | 101000 | 1,4 |
| 左上到右下( rvis) | 001011 | 3,5,6 |
| 所有禁放位置( pos ) | 111011 | 1,2,3,5,6 |
对 pos 取反得到 000100,再使用 lowbit 获取最后一个 1 的位置 。就可以得到当前能够放置棋子的位置。对应上面的图,就是位置 4 。
选择位置 4 后,递归到下一层,分别对 row,lvis,rvis 执行或运算,将位置 4 变为 1 。
同时 lvis 左移 1 位, rvis右移一位。
输入
一行一个正整数,表示 n(n<=15)
输出
输出一个正整数,表示八皇后摆放的个数
样例
输入
8
输出
92