你有一个含 n 个点、m 条边的图。现在选出一棵生成树，你每次可以选择树上一条边使其边权 -1，问至少需要操作多少次之后这棵树会成为图的最小生成树？

保证图完全连通且不含重边。（注：图中节点编号从 1 ~ n）

1. 第一行输入两个数 n、m，分别表示图的点数和边数（1 \leq n \leq 10000，1 \leq m \leq 100000）。

2. 之后 m 行，每行三个数 u、v、w，表示从点 u 到点 v 的连边权值为 w。

3. 之后 n-1 行，每行两个数 a、b，表示选定生成树的每条边。

输出一个数，表示最少的操作次数。

- 对于 25% 的数据：1 \leq n \leq 20，1 \leq m \leq 100；

- 对于 40% 的数据：1 \leq n \leq 100，1 \leq m \leq 500；

- 对于 60% 的数据：1 \leq n \leq 1000，1 \leq m \leq 5000；

- 对于 100% 的数据：1 \leq n \leq 10000，1 \leq m \leq 100000，1 \leq w \leq 1000000，1 \leq a,b \leq n。

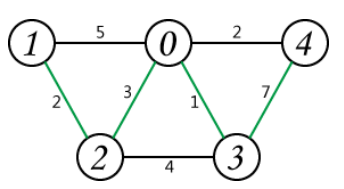
样例解释：

样例中的情况如图所示，对于选定的树，只要将 3-4 边的权值改为 2 即可成为最小生成树，操作次数为 5。