某校大门外长度为 L 的马路上有一排树，每两棵相邻的树之间的间隔都是 1 米。

我们可以把马路看成一个数轴，马路的一端在数轴 0 的位置，另一端在 L 的位置；数轴上的每个整数点，即 0,1,2,\dots,L 都种有一棵树。

由于马路上有一些区域要用来建地铁。这些区域用它们在数轴上的起始点和终止点表示。已知任一区域的起始点和终止点的坐标都是整数，区域之间可能有重合的部分。现在这些区域中的树（包括区域端点处的树）已经被移走了。

如果我们把所有间隔为 1 的树连接起来，那么显然剩下的所有树被分割成了很多段。如果某段包含了大于等于 x 棵树，33DAI 就可以在这一段树下睡觉。请问 33DAI 有多少位置可以睡觉。

第一行有三个整数 L、M、x，（M 代表区域的数目，L,x 的含义如题目描述所述）。

接下来的 M 行每行包含两个不同的整数，第 i 行为第 i 个区域的起始点和终止点的坐标 l_i, r_i 。

包括一行，这一行只包含一个整数，表示 33DAI 有多少位置可以睡觉。

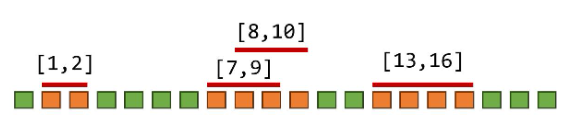
如图，样例 1 中，剩下的树被分为了四段，长度分别为 1,4,2,3，有两段满足长度大于等于 x(3)，所以输出 2。

数据范围

对于 100\% 的数据，保证 1\le x,L\le 5000，1\le M\le 100，0\le l_i\le r_i\le L。

- 子任务 1（30 分）：保证 x=1

- 子任务 2（30 分）：保证 l_i=r_i

- 子任务 3（40 分）：没有特殊的限制。