有一个网格，网格中有 H 行和 W 列。让 (i,j) 表示从上往下第 i 行和从左往上第 j 列的单元格。

如果 S_{i,j} 是`#`，则 (i,j) 单元格无法通过；如果是`.`，则该单元格可以通过且不包含房屋；如果是`@`，则该单元格可以通过且包含房屋。

起初，圣诞老人在单元格 (X,Y) 。他将根据字符串 T 进行行走。

- 假设 |T| 是字符串 T 的长度。对于 i=1,2,\ldots,|T| ，他的行走路线如下。

    - 假设 (x,y) 是他目前所在的单元格。

        - 如果 T_i 是 "U"，且 (x-1,y) 单元格可以通过，则移动到 (x-1,y) 单元格。

        - 如果 T_i 为 "D "且 (x+1,y) 格可以通过，请移至 (x+1,y) 格。

        - 如果 T_i 为 "L "且 (x,y-1) 格可以通过，请移动到 (x,y-1) 格。

        - 如果 T_i 是 "R"，且 (x,y+1) 单元格可以通过，则移动到 (x,y+1) 单元格。

        - 否则，停留在 (x,y) 格。

找出他完成所有行动后所在的单元格，以及他在行动过程中经过或到达的不同房子的数量。如果多次经过同一间房子，则只计算一次。

 第一行给定四个数字，分别表示H 行和 W 列，起点单元格 (X,Y) ；

接下来一个H 行和 W 列的迷宫地图；

最后一行，表示圣诞老人的行动路线，里面'UDLR'组成。

假设 (X,Y) 是他完成所有操作后所在的单元格，而 C 是他在操作过程中经过或到达的不同房子的数量。按此顺序打印 X,Y,C 并用空格分隔。

圣诞老人的行为如下

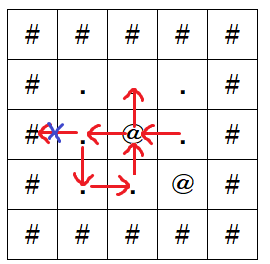
- T_1= L`，因此他从 (3,4) 移动到 (3,3) 。过了一户人家。

- T_2= L，所以他从 (3,3) 移动到 (3,2) 。

- T_3= L，但是 (3,1) 单元无法通过，所以他停留在 (3,2) 。

- T_4= "D"，所以他从 (3,2) 移动到 (4,2) 。

- T_5= "R"，因此他从 (4,2) 移动到 (4,3) 。

- T_6= U`，因此他从 (4,3) 移动到 (3,3) 。过了一户人家，但是已经过了一户人家。

- T_7= U`，所以他从 (3,3) 移动到 (2,3) 。

他在行动中经过或到达的房屋数为 1 。

- 3 \leq H,W \leq 100

- 1 \leq X \leq H

- 1 \leq Y \leq W

- 所有给定的数字都是整数。

- 每个 S_{i,j} 都是 `#`、`.`、`@` 中的一个。

- S_{i,1} 和 S_{i,W} 是每个 1 \leq i \leq H 的 `#`。

- S_{1,j} 和 S_{H,j} 是每个 1 \leq j \leq W 的 `#`。

- S_{X,Y}= `.`

- T 是长度至少为 1 且最多为 10^4 的字符串，由 `U`、`D`、`L`、`R` 组成。