(24-25赛季)稠州常规赛06
P4. 排列的和permutation
描述
给了你一个正整数 n,你需要对每个 s = 0, 1, 2, \dots, n^2,求出有多少个 1 \sim n 的排列 p,满足:
\sum_{ i= 1}^nmax(i, p_i) = s
答案对 P 取模。
输入
一行两个正整数 n, P
输出
输出一行 n^2 + 1个非负整数,用空格分开,表示 s = 0, 1, 2, \dots, n^2的答案。
样例
输入
3 100
输出
0 0 0 0 0 0 1 2 3 0
输入
4 114514
输出
0 0 0 0 0 0 0 0 0 0 1 3 7 9 4 0 0
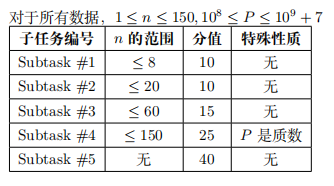
提示
样例1解释:
共有 6 个排列:
p = (1, 2, 3) 有 \sum_{i = 1}^nmax(i, p_i) = 6
p = (1, 3, 2) 有 \sum_{i = 1}^nmax(i, p_i) = 7
p = (2, 1, 3) 有 \sum_{i = 1}^nmax(i, p_i) = 7
p = (2, 3, 1) 有 \sum_{i = 1}^nmax(i, p_i) = 8
p = (3, 1, 2) 有 \sum_{i = 1}^nmax(i, p_i) = 8
p = (3, 2, 1) 有 \sum_{i = 1}^nmax(i, p_i) = 8
提交
题目参数
| 时间限制 | 3 秒 |
| 内存限制 | 512 MB |