- 给出一个 n 个点的有根树，节点编号为 1, 2, \cdots n，树根为 1，第 i（2 \le i \le n）号节点的父亲是 p_i。

- 给出 q 个查询，第 i 个查询包含 a_i, b_i，计算满足以下条件的点 u 的个数：

1. a_i 位于 u 到 1 的最短路径上（端点也算）；

2. u 到根上的路径恰好有 b_i 条边。

第一行一个数字N;

第二行N-1个数字，表示第i+1个节点的父节点P_i;

第三行一个数字Q;

接下来Q行，每行两个数字 U_i 和 D_i 

给出每次查询符合的节点数

数据范围：

—— 2 \leq N \leq 2 \times 10^5

—— 1 \leq P_i < i

—— 1 \leq Q \leq 2 \times 10^5

—— 1 \leq U_i \leq N

—— 0 \leq D_i \leq N - 1

—输入的所有值均为整数。

样例解释：

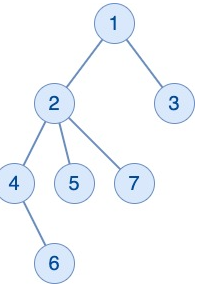
在第1 次查询中，顶点 4 、 5 和 7 满足条件。

在 第2 次查询中，只有 7 顶点满足条件。

在 第3 次和 4次查询中，没有顶点满足条件。