大唐藏经阁的地图类拥有n本地图册。

藏经阁想为地图类的所有书制作一个书架，并想让书架的长宽尽量小。第i本书的厚度是v[i]，且这本书的纸张宽度是w[i]。书的厚度是1或2，所有书都有同样的高度（即书架的高是均匀的）。

藏经阁的官员想了以下的方式摆放这些书籍。

>1.他选择了一些书并竖直摆放它们。

>2.他将剩余的书籍水平放置于竖直的书上面。

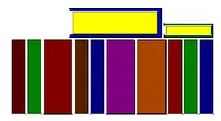
水平放置的书的宽度和不能多于竖直放置的书的总厚度。图中描绘了书籍的样本排列。

帮助藏经阁找到可以达到的书架长度最小值minlen。

输入的第一行包含一个整数n。

下面的n行分别为v[i]和w[i]，对应了书的长度和宽度（即书籍竖直放置与水平放置所占的空间）。

（1<=t[i]<=2,1<=w[i]<=100)

一个整数，为可以达到的最小的长度。

30%数据，6\leq n \leq 20

100%数据，n \leq 500,总厚度 \leq 10^5