0917日常周赛
There is a directed graph with
N vertices and N edges.
The i-th edge goes from vertex i to vertex Ai. (The constraints guarantee that i!=A i.)
Find a directed cycle without the same vertex appearing multiple times.
It can be shown that a solution exists under the constraints of this problem.
Notes
The sequence of vertices B=(B1,B2 ,…,BM ) is called a directed cycle when all of the following conditions are satisfied:
1,M≥2
2,The edge from vertex Bi to vertex Bi+1exists. (1≤i≤M−1)
3,The edge from vertex BM to vertex exists.
4,If i!=j, then Bi!=Bj.
Constraints
All input values are integers.
2≤N≤2×10^5
1≤Ai≤N,Ai!=i
The input is given from Standard Input in the following format:
N
A1,A2...AN
Print a solution in the following format:
M
B1,B2....BN
M is the number of vertices, and Bi is the i-th vertex in the directed cycle.
The following conditions must be satisfied:
2≤M
B_i+1=A_Bi( 1≤i≤M−1 )
B_1=A_BM
Bi!=Bj(i!=j)
If multiple solutions exist, any of them will be accepted.
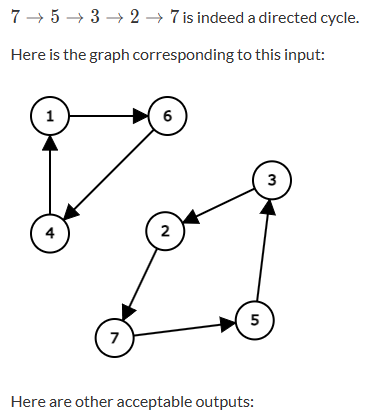
输入
7 6 7 2 1 3 4 5
输出
4 7 5 3 2
输入
2 2 1
输出
2 1 2
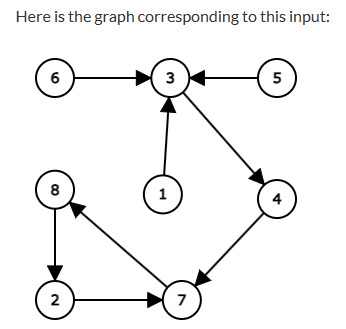
输入
8 3 7 4 7 3 3 8 2
输出
3 2 7 8
1
2

3
| 时间限制 | 1 秒 |
| 内存限制 | 128 MB |